Matte!
Ursäkta! Vet inte om det är ett typa, men sista termen, 2*180*180*cos(55) ska vara 2*120*180*cos(55). Det är ju 2*b*c*cos(55), där b=120 och c=180
Finns det något sätt man kan dubbelkolla så man räknat rätt när det gäller att hitta längden på en sida av en triangel?
"I en triangel är två sidor 180mm respektive 120mm och mellanliggande vinkel är 55 grader. Hur stor är triangelns tredje sida?"
Hur vet jag att jag fått fram rätt svar om jag påstår att den är 148mm?
(Sorry, redigerade. Såg nu att jag inte hur jag än knappade på miniräknarn fick det till 98 igen... vet inte hur fel jag tröck nyss..)
Det kan vara svårt att kolla. Finns några sätt, men de tar alla fler steg än den faktiska uträkningen, varvid det är en än större risk att knappa in fel.
Det jag brukar göra är att dela upp uträkningen i dess termer. Först räknar man ut 120^2, sen 180^2 , sen 2*120*180*cos(55), varefter man kan kan skriva in det helt numeriskt.
I det här fallet är svaret 148.
Det finns ett uppenbart sätt att kolla: rita triangeln och mät.
Om man har verktyg för att mäta vinkeln är det såklart ett bra sätt.
Man kan höfta vinkeln utan verktyg. Det är aldrig en bra idé att tro att ens bilder ger exakt korrekta svar, så man bör bara se bilderna som en kontroll av huruvida ens svar är in the ballpark. Har man inga verktyg? Ptja, måla bilden så bra du kan och ha helt enkelt en större ballpark. Är längden på tredje sidan i den målade triangeln runt 140-160 mm så är 148 mm troligen korrekt.
ska tillbaka till matematik världen snart igen gissar jag.
Måste plugga upp Matematik D eller 4 vad det nu heter..
Holy shite. I min kurs multilinjär algebra togs the Grassmannian upp i förbifarten. Säg att du har ett n-dimensionellt vektorrum V och låt k vara ett heltal mindre än n. Då utgörs the Grassmannian Gr(k, V) av mängden av alla k-dimensionella delrum till V. Så varje k-dimensionellt delrum till V är en punkt i Gr(k, V).
Som exempel är Gr(1,V) mängden av alla linjer genom origo, AKA det projektiva rummet över V. På samma sätt är Gr(2,V) mängden av alla plan som går genom origo, osv.
Om V är ett reellt eller komplext vektorrum så är Gr(k, V) så kallade compact, smooth manifolds. Så dessa rum bestående av delrum till något vektorrum har geometriska, ganska snälla egenskaper. Galet värre.
Vet att detta är mer åt fysikhållet men om någon skulle kunna hjälpa ändå skulle det uppskattas!


Kan hjälpa dig med den första, men minns inte det där med fältstyrkan från jordens gravitation.
Begynnelsehastighet har komposanterna v0x = v0 * cosvinkeln och v0y = v0 * sinvinkeln.
7.5 * cos40 = 5.75
7.5 * sin40 = 4.82
Hastighetsformlerna lyder som vx = v0x och vy = v0y -gt. Hastighetsresultaten i varje ögonblick kan ges av pythagoras sats. Vres = (vx^2 + vy^2)^0.5
vx = 5.75 m/s
vy = 4.82 - 9.82*0.5 = -0.09 m/s
Vy har alltså negativ riktning, men beräknas fortfarande som positiv.
vres = (5.75^2 + 0.09^2)^0.5 = 5.75 m/s
Lägesformlerna lyder som x = v0x * t och y = v0y * t - 1/2 * g*t^2
Delta-y för kast är 1.75m
x = 5.75 * 0.5 = 2.875 m
y = 1.75 + 4.82 * 0.5 - 1/2 * 9.82*0.5^2 = 2.9325 m
Vi kan räkna ut tiden för när y = 0 genom 1.75 + 4.82t - 1/2 * 9.82t^2 = 0
1.75 + 4.82t - 4.91t^2 = 0
- 0.356 - 0.982t + t^2 = 0
t = 0.491 +- (0.241 + 0.356)^0.5
t = 0.491 +- 0.773
t = 1.264
Definitionsmängden tillåter bara ett t.
Tiden genom sträckformeln för x ger:
5.75 * 1.264 = 7.27 m
Fråga två är en trickfråga, bortse från solens inverkan till att börja med. Punkten där L2 ligger sett från Jorden kallas den geostationära punkten. Det avståndet är alltid konstant för alla objekt som sätts i ombana.
Börja med att titta på m*a = m *g eftersom satelliten då hålls stilla på den höjden.
där a= w^2*r (där r=satelitens avstånd från jorden, w= satelitens rotationshastighet runt jorden [rad/sek] ) (alltså centripetal accelerationen)
g = (M*G)/r^2 (G= 6.674*10^-11 gravitationskonstanten, M = jordens massa, r=samma som ovan) (alltså jordens attraktionsaccelleraftion (inte kraft!))
Du är ju här intresserad av att hitta r. Avståndet alltså. Så lös ut det.
Igår kom jag på ett bra sätt att förklara för lekmän var rigorisiteten kommer in när man forskar i matematik:
Tänk dig att du ska flytta till en ny lägenhet, du har en bild på planlösningen framför dig och försöker komma fram till en bra möblering. Du börjar med att skissa, "kan ställa soffan ungefär hääär, sängen dääär, längsmed den väggen ser mina bokhyllor ut att passa perfekt", men det är inte förrän du har kommit fram till en bra möblering som du plockar fram tumstocken och undersöker huruvida alla möbler faktiskt får plats på sin tänkta position. Du behöver bara noggrant mäta sådana möbler som ska stå på trånga ställen.
På samma sätt forskar man i matematik. Först kommer idéerna, intuitionen, från vilka man målar upp skisser. När man tror sig ha kommit fram till något så kontrollerar man detaljerna, och hur teknisk den kontrollen blir beror på hur slarvig din skiss är och hur mycket svängrum som finns för dina slutsatser att vara korrekta.
Lös ekvationen tan(x-05)=1, svara i radianer med två decimaler.
Vet inte alls hur jag ska gå till väga för att få loss x:et ur parentesen..
Kan någon ge mig en liten knuff..
Citat från saxx:
Lös ekvationen tan(x-05)=1, svara i radianer med två decimaler.
Vet inte alls hur jag ska gå till väga för att få loss x:et ur parentesen..
Kan någon ge mig en liten knuff..
Dels kan man använda arctan, det är den s.k. inversa funktionen till tan. Men kan kan också tänka såhär:
tan t = sin t / cos t, så tan t = 1 innebär att sin t = cos t. Har ni arbetat något med enhetscirkeln? På enhetscirkeln ger cos t x-värdet och sin t y-värdet, där t är vinkeln (mätt i radianer, t ex) mellan x-axeln och linjen från (0,0) till (cos t, sin t) = (x,y).
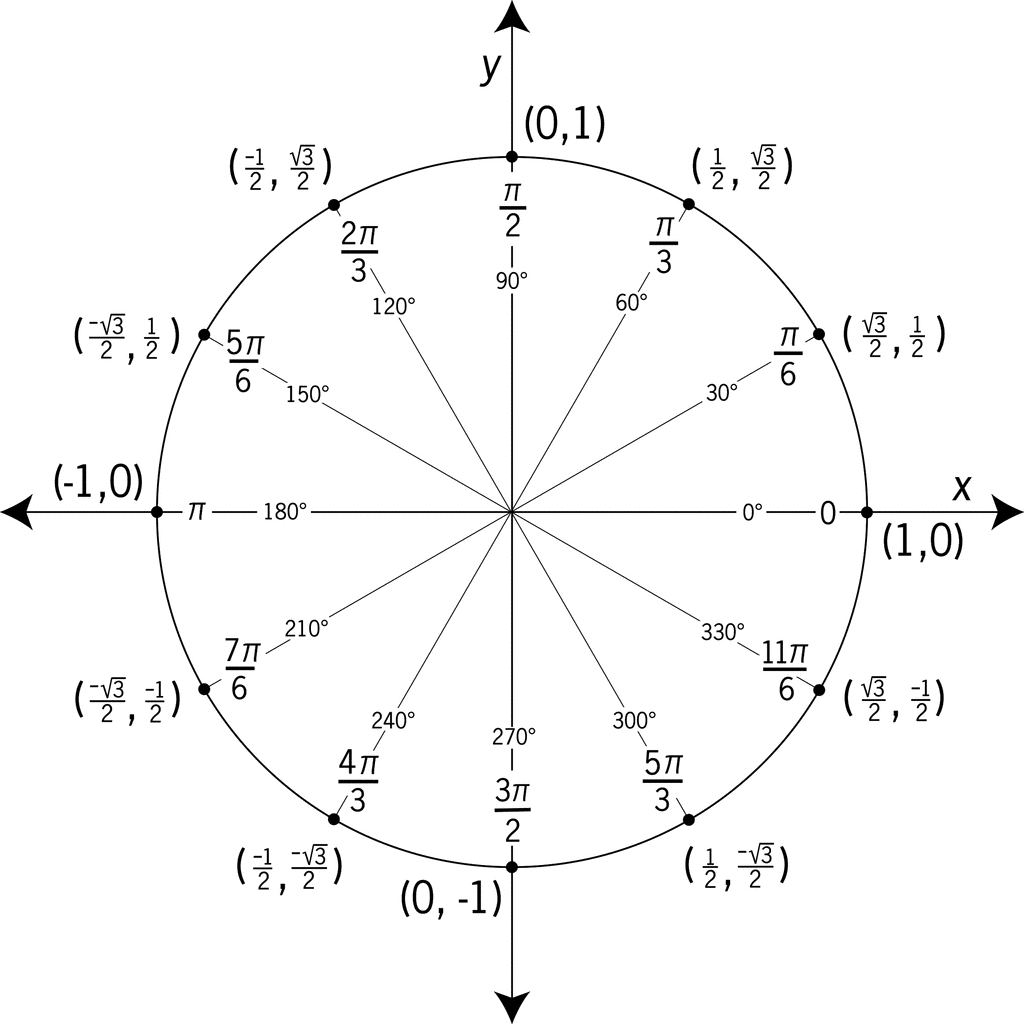
Exempel: cos(pi/3) = 1/2, sin(pi/3) = sqrt(3)/2. Så vinkeln pi/3 motsvarar punkten (1/2, sqrt(3)/2) på enhetscirkeln - som bilden visar.
Så likheten sin t = cos t innebär att punkten (cos t, sin t) på enhetscirkeln har samma x-värde som y-värde. Det finns två såna punkter, så det finns två lösningar på ekvationen ovan (om man bara tittar på radianer mellan 0 och 2pi). Finn de två motsvarande vinklarna t.
arctan i båda led, du får ett värde för arctan(1) och sen är det bara att lösa ut som en vanlig ekv
som jimmy skrev får du 2 värden men om inget är angivet får du skriva generellt som x = v + n * pi där v är vinkeln och n är ett godtyckligt heltal
Du måste vara inloggad för att skriva i forumet