Matte!
Citat från Titan:
Hade samma prov, skrattade lite. Fick precis den uppgiften 1 vecka tidigare av min mattelärare :~)
Vi hade inte fått någon uppgift tidigare som liknade dessa :(
Juste, hehe, jag lyckades på något jävla sätt svara fel på första frågan om temperaturskillnader... hehe... Dags att börja dubbelkolla sina svar xd
Citat från synshadows:
Jag har suttit ett litet tag och försökt hitta en approximativ funktion till den primitiva funktionen till standardnormaltäthetsfunktionen. Detta är inom sannolikhet då. I fantasin tycker jag att ArcTan borde kunna användas och jag har fått fram typ 0.0338937 + 0.368637 ArcTan[x] men det är ändå långt ifrån en bra approximation. Observera att jag alltså bara försöker hitta täthetsfunktionens primitiv från o till oändligheten.
En liten bild på hur den borde se ut, har plottat en massa punkter så rent grafiskt ska den se ut exakt såhär:
Bild: https://dl.dropboxusercontent.com/u/60721268/plooootttt.gif
Läs lite här: http://en.wikipedia.org/wiki/Normal_distribution#Cumulative_distribution_function
Tydligen går det att approximera med serieutvecklingen
F(x) = 0.5 + e^(-x²/2)/sqrt(2pi) sum{ x^(2k + 1)/k!!, n st termer
Tack, den kan jag säkert använda faktiskt!
Tjo!
Min mattelärare har fått för sig att alla måste lösa vars en uppgift på tavlan, problemet är att han har lagt uppgifterna på en något för svår nivå, och jag fattar inte hur jag ska lösa den. Den som kan hjälpa mig är typ världens bästa person!
Uppgiften:
En snöboll smälter i vårsolen med 1,5 cm^3/minut. Bestäm hur snöbollens radie minskar då denne är 6 cm.
Citat från DroppSaft:
Tjo!
Min mattelärare har fått för sig att alla måste lösa vars en uppgift på tavlan, problemet är att han har lagt uppgifterna på en något för svår nivå, och jag fattar inte hur jag ska lösa den. Den som kan hjälpa mig är typ världens bästa person!
Uppgiften:
En snöboll smälter i vårsolen med 1,5 cm^3/minut. Bestäm hur snöbollens radie minskar då denne är 6 cm.
Visa mig vad du har förstått av uppgiften eller vad du har gjort hittills.
https://dl.dropboxusercontent.com/u/60721268/Sn%C3%B6bollen2.pdf
Okej, så har gjort en ganska lång lösning på uppgiften här. Skrev uttrycken på datorn så det är väldigt mycket parenteser på vissa ställen. Om du inte har problem med att läsa sånt så har du hela lösningen I en pdf-fil I länken : )
Om du vill att jag skriver ut något för hand eller vill ha nån förklaring så är det bara att fråga. Men sitter inte vid datorn igen förän I eftermiddag. Tror du kan ha hjälp av det ändå. Men lite arbete krävs av dig själv också om du vill visa deriveringssteg osv men annars star allt där ; >
observera, har förenklat visa uttryck I min lösning här, omredigerat kl 19:48 idag
Citat från DroppSaft:
Tjo!
Min mattelärare har fått för sig att alla måste lösa vars en uppgift på tavlan, problemet är att han har lagt uppgifterna på en något för svår nivå, och jag fattar inte hur jag ska lösa den. Den som kan hjälpa mig är typ världens bästa person!
Uppgiften:
En snöboll smälter i vårsolen med 1,5 cm^3/minut. Bestäm hur snöbollens radie minskar då denne är 6 cm.
glömde citera, lösning finnes ovan
eventuellt finns en enklare lösning om man redan från början antar att minskningen vid radie=6 inte påverkas av hur stor den var från början. Kan kanske skriva den när jag kommer hem.
Jag ville gärna se var behövde hon hjälp och inte ge direkt lösning till henne, i vissa fall behöver de bara en lite förklaring eller de fastnar i mitten av uppgiften. Vi är här för att hjälpa och inte göra läxor åt dem.
Du får mina lösningar i alla fall.
http://s29.postimg.org/h9tkgzts7/DSC_0295.jpg
Citat från synshadows:
du har skrivit "utlösning" i din uträkning nånstans där, tänkte bara uppmana till att inte uttrycka sig på det viset vid en muntlig presentation inför klassen. har begått det misstaget förut och skulle helst undvika det :--------)
f.ö. vore det nog smidigast att bara hänvisa till kedjeregeln direkt som ovanstående gjorde
Tack så jättemycket! Ni är helt underbara!
Har ett litet typ matteproblem. Är ingenting som har med skola eller något att göra utan det är så att jag jobbar som VVSare och i jobbet bockar man mycket rör (uppenbarligen). till mitt lilla "problem" då, Det finns vissa typ k-värden för olika bockningsgrader, till exempel om jag vill göra en S-bock på 45 grader och det ska vara 10 cm från centrum till centrum rör så tar jag 10x1,41 och vet då att om jag märker på "0" och 14,1 cm och använder samma markering på bockverktyget så kommer jag få en S-bock på 10cm, har även k-värden för 15, 30 och 60 grader; 3,86 - 2,0 samt 1,15.
Min fråga är alltså hur har man räknat ut detta k-värde?
skulle nämligen vilja kunna räkna ut k-värdet för exempelvis 37 grader.
Kan tilläggas att dessa värden inte är beroende av vilken rördimension eller vilket typ av bockverktyg man använder och man kan alltså använda samma värden för 28mm som för 15mm-rör trots markant skillnad i bockningsradie.
Någon med större mattekunskaper än en själv som förstår vad jag menar och orkar ge sig på detta?
bild på en S-bock:
Jag har försökt lösa problemet men har inte hittat rätt lösning via varken geometriskt resonemang eller numerisk beräkning. Nu måste jag sova, så tyvärr kan jag inte försöka mer.
Citat från Jimmy:
Jag har försökt lösa problemet men har inte hittat rätt lösning via varken geometriskt resonemang eller numerisk beräkning. Nu måste jag sova, så tyvärr kan jag inte försöka mer.
förklarade säkert lite luddigt.
Beroende på om jag vill bocka i 15, 30, 45 eller 60 grader använder jag alltså olika k-värden, som inte har något med längden att göra.
alltså
15 grader = 3,86
30 grader = 2,0
45 grader = 1,41
60 grader = 1,15
Så om jag exempelvis ska bocka 10 cm kan jag göra såhär
10 x 3,86 = 38,6 cm
10 x 2,0 = 20 cm
10 x 1,41 = 14,1 cm
10 x 1,15 = 11,5 cm
dessa mått blir ju då alltså måttet mellan bockarna
Alltså varje gradtal har ju då ett specifikt k-värde och jag vill ha fram hur man räknar ut det för vilket gradtal som helst.
Bifogar en liten ritning där jag försökt illustrera vad jag menar.
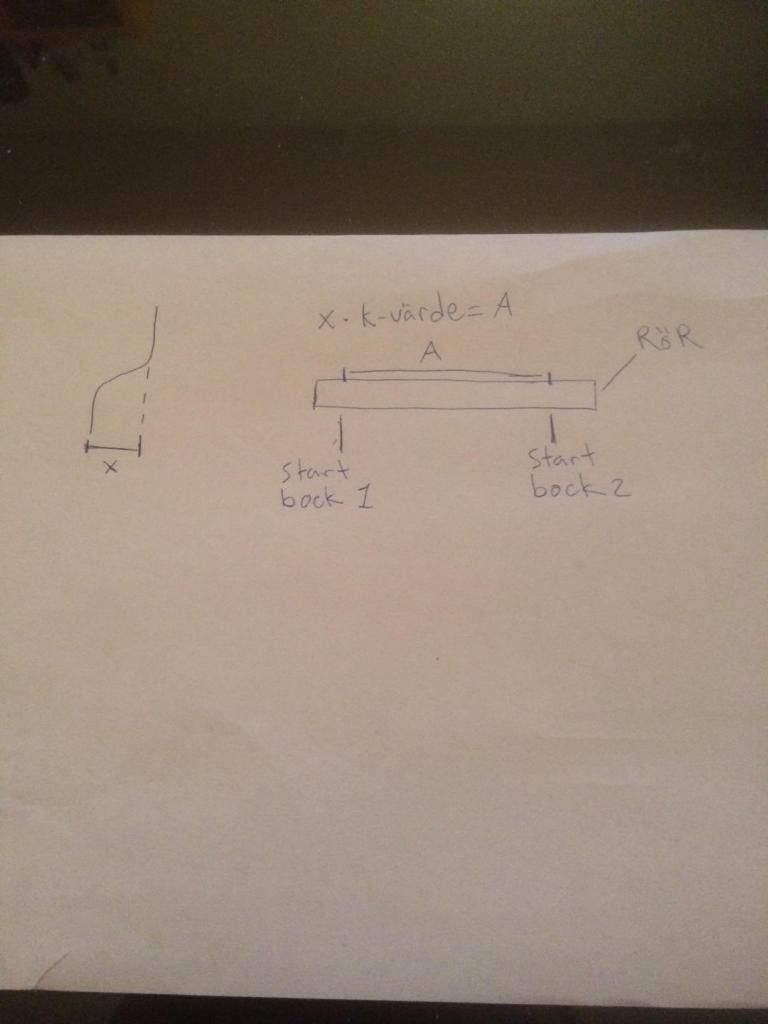
Försökte lite för ett tag sen, men är förmodligen helt fel ute men kom i alla fall fram till
sin(60) x 1,33 = 1,15
sin(45) x 2 = 1,41
sin(30) x 4 = 2,0
sin(15) x 14,9 = 3,86
Jag skulle behöva lite mattehjälp till o lösa lite fysik.
Bara som exempel:
Om vi har ett accelerationsfält F=(-x/sqrt(x^2+y^2) , -y/sqrt(x^2+y^2))
och sedan lägger en partikel I nån punkt, tex (0, 6)
sedan skjuter vi ut partikeln med hastigheten (100, 0) (det är alltså hastighetsvektorn)
Hur kan jag tar reda på partikelns position samt dess nya hastighetsvektor efter en viss tid i den nya punkten?
Jag inser att jag har problem eftersom jag inte har någon funktion av t nånstans men kommer inte riktigt på hur en sån kan komma in här : /
Du måste vara inloggad för att skriva i forumet
